cosmo_derived

This plugin calculates the following “derived” cosmological quantities: * \(H(z)\) * \(D_A(z)\) * \(r_s(z)\) * \(\theta_s(z)\) * \(z_{\rm drag}\) (Hu & Sugiyama fitting formula)

It can also be used as a \(\theta\) to \(H_0\) converter.

Credit: Lloyd Knox, code adapted by Marius Millea

from cosmoslik import *

cosmo_derived = get_plugin('models.cosmo_derived')()

To use cosmo_derived, first call the set_params function to set all the cosmological parameters, then call the other functions which will subsequently use those values. Here’s the signature for set_params:

help(cosmo_derived.set_params)

Help on built-in function set_params:

set_params(...) method of cosmoslik_plugins.models.cosmo_derived.cosmo_derived._cosmo_derived instance
    _cosmo_derived.set_params(self, H0=None, theta_mc=None, ombh2=None, omch2=None, omk=None, mnu=None, massive_neutrinos=None, massless_neutrinos=None, Tcmb=None, Yp=None, **kwargs)

    Args:
        H0 : hubble constant today in km/s/Mpc
        ombh2, omch2, omk : densities today
        mnu : neutrino mass sum in eV
        massive_neutrinos : number of massive species (mnu divided equally among them)
        massless_neutrinos : number of massless species
        Yp : helium mass fraction
        Tcmb : CMB temperature in Kelvin
        theta_mc : if given, will convert to H0 and set H0 to that

cosmo_derived.set_params(H0=67.04, ombh2=0.022032, omch2=0.12038, omk=0, mnu=0.06, massive_neutrinos=1, massless_neutrinos=2.046)

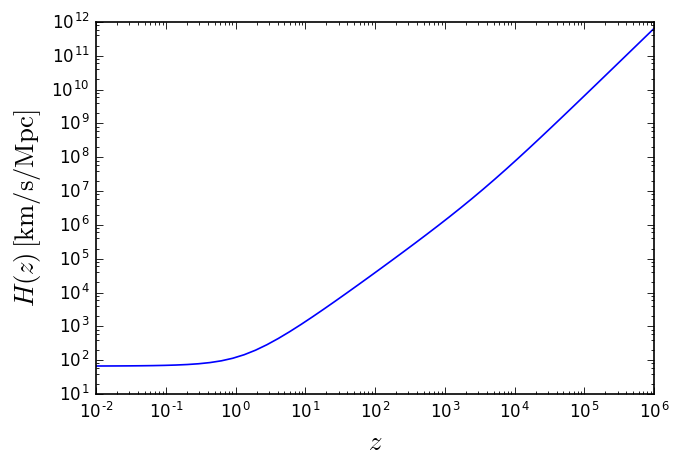
Plotting \(H(z)\),

z=logspace(-2,6)
loglog(z,list(map(cosmo_derived.Hubble,z)))
xlabel(r'$z$',size=16)
ylabel(r'$H(z) \, [\rm km/s/Mpc]$',size=16);

Here’s the angular size of sound horizon at Planck’s best-fit \(z_*\) (Table 2, Planck XVI). The number for \(\theta_s\) in that same table is \(0.0104136\), or a difference of \(0.09 \sigma\). This is likely due to differences in numerical values for physical constants that were used, or numerical integration error.

z_star = 1090.48
cosmo_derived.theta_s(z_star)

0.010414141562032136

We can also use this plugin to convert \(\theta\) to \(H_0\). Here \(\theta\) refers to \(\theta_{\rm MC}\) which uses the Hu & Sugiyama fitting formula for \(z_{\rm drag}\).

cosmo_derived.theta2hubble(0.0104)

66.95260969910498

This plugin is written in Cython and is highly optimizied, so its pretty fast.

%%timeit
cosmo_derived.theta_s(z_star)

100 loops, best of 3: 9.16 ms per loop

%%timeit
cosmo_derived.theta2hubble(0.0104)

10 loops, best of 3: 56 ms per loop

The \(\theta_s\) calculation about 7 times slower than the equivalent Fortran code used in CosmoMC. The theta to hubble conversion is about 3 times faster than the CosmoMC version because the equation solver is more sophisticated and requires fewer \(\theta_s\) evaluations. Not bad for being very readable and modifiable Cython code instead. As an example, here’s what the code looks like:

def r_s(self, double z):
    """
    Returns : comoving sound horizon scale at redshift z in Mpc.
    """
    cdef double Rovera=3*self.ombh2*rhoxOverOmegaxh2/(4*self.rhogamma0)
    return quad(lambda double zp: 1/self.Hubble(zp) / sqrt(3*(1+Rovera/(1+zp))),z,inf,epsabs=0,epsrel=self.epsrel)[0] / KmPerSOverC